An alphabet is a finite, nonempty set Σ of symbols.
For example:
Σ = {a, b}
or
Σ = {0, 1}
or
Σ = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z}
A string is a sequence of symbols from Σ.
It is common to use variables to name strings. For example:
u = baa
w = abba
It should be noted that the following statements are true about these strings.
baa ∉ Σ
baa ϵ Σ*
Recall that Σ* is the alphabet which contains lambda (λ). λ is the empty string. It represents a string with the length of 0.
The reason that baa ∉ Σ but baa ϵ Σ* is because Σ* represents every possible combination of the elements {a, b} of Σ.
For Σ = {a, b}, Σ* is countably infinite.
We can show the ordered lexicography of Σ* by writing the elements of Σ* our as {λ, a, b, aa, ab, ba, bb, aaa, aab, aba, ...}.
Concatination
uw = baaabba
uu = baabaa
For any integer n >= 0, un is the string u, concatenated n times. For example:
un = uuu...u
u3 = baabaabaa
Theo's Math Journal
Saturday, December 31, 2016
Friday, April 22, 2016
Functions in computation
A function is a rule that assigns one element to a unique (one and only one) element.
Examples
S1 = {a, b, c}
S2 = {w, x, y, z}
f: S1 --> S2
Function or not?
f1 = {(a, x), (b, z), (a, y)} Function
f2 = {(a, x), (a, y), (b, z)} Not a function
The example f2 is not a function because the element a maps to more than one other element. In this example, a maps to both x and y so f2 cannot be a function.
f3 = {(c, x), (b, z), (a, y)} Function
The example f3 is a function, in fact, f3 is a specific type of function called a total function.
Some other important characteristics about f3 that we can not are:
- f3 is not one-to-one. We can see this because both a and c map to x.
- f3 is not onto. We know this because some elements, such as y are not assigned to.
f4 = {(a, x), (b, y)} Function
The function f4 is a partial function. We know this because the domain of this function is {a, b} which is a proper subset. We often see this written in the notation ({a, b} ⊂ S1).
If f: S1 --> S2 is a rule for which any element of S1 is assigned at most one element of S2.
If the domain of f is a proper subset of S1, we say that f is a partial function.
If the domain of f is equal to S1, then f is a total function.
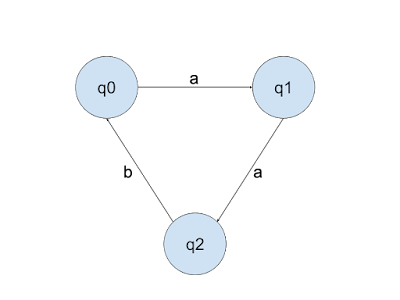
Let Q = {q0, q1, q2} A = {a, b}
Define f: Q x A --> Q as follows:
(q0, a) --> q1
(q1, a) --> q2
(q2, b) --> q0
(q1, b) --> q1
This is a partial function, not a total function. This is because the function does not include rules for all 6 possible transitions. This may be easier to see if we create a state diagram to illustrate this function.
The state diagram for this function makes it easier to see that there are transition rules missing from the function that we have defined. For example, starting in q0, it is not possible to process the string abaa. We can however process strings like aabab. This function is called non-deterministic. A deterministic function would have rules that describe what to do at each state for each element.
Examples
S1 = {a, b, c}
S2 = {w, x, y, z}
f: S1 --> S2
Function or not?
f1 = {(a, x), (b, z), (a, y)} Function
f2 = {(a, x), (a, y), (b, z)} Not a function
The example f2 is not a function because the element a maps to more than one other element. In this example, a maps to both x and y so f2 cannot be a function.
f3 = {(c, x), (b, z), (a, y)} Function
The example f3 is a function, in fact, f3 is a specific type of function called a total function.
Some other important characteristics about f3 that we can not are:
- f3 is not one-to-one. We can see this because both a and c map to x.
- f3 is not onto. We know this because some elements, such as y are not assigned to.
f4 = {(a, x), (b, y)} Function
The function f4 is a partial function. We know this because the domain of this function is {a, b} which is a proper subset. We often see this written in the notation ({a, b} ⊂ S1).
If f: S1 --> S2 is a rule for which any element of S1 is assigned at most one element of S2.
If the domain of f is a proper subset of S1, we say that f is a partial function.
If the domain of f is equal to S1, then f is a total function.
Let Q = {q0, q1, q2} A = {a, b}
Define f: Q x A --> Q as follows:
(q0, a) --> q1
(q1, a) --> q2
(q2, b) --> q0
(q1, b) --> q1
This is a partial function, not a total function. This is because the function does not include rules for all 6 possible transitions. This may be easier to see if we create a state diagram to illustrate this function.
The state diagram for this function makes it easier to see that there are transition rules missing from the function that we have defined. For example, starting in q0, it is not possible to process the string abaa. We can however process strings like aabab. This function is called non-deterministic. A deterministic function would have rules that describe what to do at each state for each element.
Prove 1 + 2 + 3 + ... + n = n(n+1) / 2 for all n >= 1
Background: This proof is often used for the analysis of various algorithms.
Example: 1 + 2 + ... + 100 = (100 * 101) / 2
If we wanted to write this equality as a part of a program, it could be created as either of the following snippets.
sum = 0
for i = 1 to 100:
sum += i
print sum
which is the same as
print n * (n + 1) / 2
Both of these code snippets print the same value at the end, and it is possible to mathematically prove which is more efficient.
Now, without further adieu, here is a proof that demonstrates how we can show this.
Prove: 1 + 2 + 3 + ... + n = (n (n + 1)) / 2 for all n ≥ 1.
Base case: Observe 1 = (1 * 2) / 2.
Let k ≥ 1 be some integer.
Assume 1 + 2 + 3 + ... + k = (k (k + 1)) / 2
We want to show that 1 + 2 + 3 + ... + k + (k + 1) = ((k + 1) * (k + 2)) / 2.
Notice that 1 + 2 + ... + k + (k + 1) = (k (k + 1)) / 2 + k + 1 = ((k + 1) * (k + 2)) / 2.
((k + 1) * (k + 2)) / 2 = (k (k + 1)) / 2 + 2 (k + 1) / 2
= (k (k + 1) + 2 (k + 1))
= ((k + 1)(k + 2)) / 2
By the proof of mathematical induction, 1 + 2 + 3 + ... + n = (n (n + 1)) / 2 for all n ≥ 1.
From here: Using this same proof technique, it is possible to demonstrate that this is also true for strings. For example, we can prove that (Un)R = (UR)n.
Example: 1 + 2 + ... + 100 = (100 * 101) / 2
If we wanted to write this equality as a part of a program, it could be created as either of the following snippets.
sum = 0
for i = 1 to 100:
sum += i
print sum
which is the same as
print n * (n + 1) / 2
Both of these code snippets print the same value at the end, and it is possible to mathematically prove which is more efficient.
Now, without further adieu, here is a proof that demonstrates how we can show this.
Prove: 1 + 2 + 3 + ... + n = (n (n + 1)) / 2 for all n ≥ 1.
Base case: Observe 1 = (1 * 2) / 2.
Let k ≥ 1 be some integer.
Assume 1 + 2 + 3 + ... + k = (k (k + 1)) / 2
We want to show that 1 + 2 + 3 + ... + k + (k + 1) = ((k + 1) * (k + 2)) / 2.
Notice that 1 + 2 + ... + k + (k + 1) = (k (k + 1)) / 2 + k + 1 = ((k + 1) * (k + 2)) / 2.
((k + 1) * (k + 2)) / 2 = (k (k + 1)) / 2 + 2 (k + 1) / 2
= (k (k + 1) + 2 (k + 1))
= ((k + 1)(k + 2)) / 2
By the proof of mathematical induction, 1 + 2 + 3 + ... + n = (n (n + 1)) / 2 for all n ≥ 1.
From here: Using this same proof technique, it is possible to demonstrate that this is also true for strings. For example, we can prove that (Un)R = (UR)n.
Sunday, March 13, 2016
Binary strings of length n
Length 0: λ (lambda, the empty string)
Length 1: 0, 1
Length 2: 00, 10, 01, 11
There is a useful recursive technique for finding all strings of length n + 1 given the strings of length n. To do this, we can essentially take the first set of strings and concatenate a 0 or a 1 onto it. Give the previous example with strings of length 1 and strings of length 2 we can demonstrate the following:

Now, let's take a look at a proof by induction which proves this concept.
Prove that there are 2n binary strings of length n.
Proof by induction on n.
Base case: For λ, the length of λ represented as |λ| = 0. This means that is 1 string of length 0 because 20 = 1. There is 2 binary strings of length 1 because we can choose only 0 or 1, and 21 = 2. There are 4 binary strings of length 4 because out options are "00", "10", "01", and "11", and 22 = 4.
Based on this pattern we can see a rule that there are 2n binary strings of length n.
Inductive case: Assume that there are exactly 2n binary strings of length n. Let P(n) = 2n. Consider all the binary strings of length n+1. Each string is either in the form w0 or w1, where w is a string of length n. Then, there are exactly two strings of length n+1 for each string of length n. This means that the number of strings of length n+1 is 2 * 2n = 2n+1. This means that P(n+1) is true because P(n+1) = 2n+1.
By the proof of mathematical induction, there are 2n binary strings of length n.
Length 1: 0, 1
Length 2: 00, 10, 01, 11
There is a useful recursive technique for finding all strings of length n + 1 given the strings of length n. To do this, we can essentially take the first set of strings and concatenate a 0 or a 1 onto it. Give the previous example with strings of length 1 and strings of length 2 we can demonstrate the following:

Now, let's take a look at a proof by induction which proves this concept.
Prove that there are 2n binary strings of length n.
Proof by induction on n.
Base case: For λ, the length of λ represented as |λ| = 0. This means that is 1 string of length 0 because 20 = 1. There is 2 binary strings of length 1 because we can choose only 0 or 1, and 21 = 2. There are 4 binary strings of length 4 because out options are "00", "10", "01", and "11", and 22 = 4.
Based on this pattern we can see a rule that there are 2n binary strings of length n.
Inductive case: Assume that there are exactly 2n binary strings of length n. Let P(n) = 2n. Consider all the binary strings of length n+1. Each string is either in the form w0 or w1, where w is a string of length n. Then, there are exactly two strings of length n+1 for each string of length n. This means that the number of strings of length n+1 is 2 * 2n = 2n+1. This means that P(n+1) is true because P(n+1) = 2n+1.
By the proof of mathematical induction, there are 2n binary strings of length n.
Sunday, February 21, 2016
For all n >= 0, if |S| = n, then |2S| = 2n
For all n ≥ 0, if |S| = n, then |2S| = 2n
Proof by induction on n.
Base case: Consider a set S with 0 elements.
Then S = ∅ so 2S = {∅}.
Inductive hypothesis: Let k ≥ 0 be any integer.
Assume that any set with k elements has 2k subsets.
Let S be any set with k + 1 elements.
Suppose S = {x1, x2, x3, ..., xk, xk + m}.
The set of all subsets of S can be listed in two lists.
By the proof of mathematical induction, if |S| = n, then |2S| = 2n.
Proof by induction on n.
Base case: Consider a set S with 0 elements.
Then S = ∅ so 2S = {∅}.
Inductive hypothesis: Let k ≥ 0 be any integer.
Assume that any set with k elements has 2k subsets.
Let S be any set with k + 1 elements.
Suppose S = {x1, x2, x3, ..., xk, xk + m}.
The set of all subsets of S can be listed in two lists.
- First, list all the subsets of {x1, x2, x3, ..., xk}. (These are the subsets that do not contain xk + 1).
- Second, take each of the subsets in the first list and add xk + 1 to the subset. (These are the subsets that do contain xk + 1).
By the inductive hypothesis, there are 2k subsets in the first list and 2k subsets in the second list.
So |2S| = 2n + 2k = 21 * 2k = 2k + 1
By the proof of mathematical induction, if |S| = n, then |2S| = 2n.
Furthering this concept
This proof by induction demonstrated a method of showing that the number of elements in the power set is equal to 2 raised to the power of the number of elements in the set.
What we do not necessarily see in this proof is the fact that this is actually a recursive process.
If we take an example set S, such that S = {a, b, c}, then we should be able to make the following statements about S:
- Subsets of S that do not contain c include: ∅, {a}, {b}, {a, b}.
- Subsets of S that contain c include: {c}, {a, c}, {b, c}, {a, b, c}.
Looking back at the original problem that we proved, we can see that this remain true for S since:
- |S| = 3
- 2S = ∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}
- |2S| = 23 = 8
Since this is true, then we should be able to prove that the same is true for a set S such that S = {a, b, c, d}.
Subscribe to:
Posts (Atom)