Functions in computation

A function is a rule that assigns one element to a unique (one and only one) element.

Examples

S1 = {a, b, c}
S2 = {w, x, y, z}
f: S1 --> S2

Function or not?
f1 = {(a, x), (b, z), (a, y)} Function
f2 = {(a, x), (a, y), (b, z)} Not a function

The example f2 is not a function because the element a maps to more than one other element. In this example, a maps to both x and y so f2 cannot be a function.

f3 = {(c, x), (b, z), (a, y)} Function

The example f3 is a function, in fact, f3 is a specific type of function called a total function.
Some other important characteristics about f3 that we can not are:
- f3 is not one-to-one. We can see this because both a and c map to x.
- f3 is not onto. We know this because some elements, such as y are not assigned to.

f4 = {(a, x), (b, y)} Function

The function f4 is a partial function. We know this because the domain of this function is {a, b} which is a proper subset. We often see this written in the notation ({a, b} ⊂ S1).

If f: S1 --> S2 is a rule for which any element of S1 is assigned at most one element of S2.
If the domain of f is a proper subset of S1, we say that f is a partial function.
If the domain of f is equal to S1, then f is a total function.

---

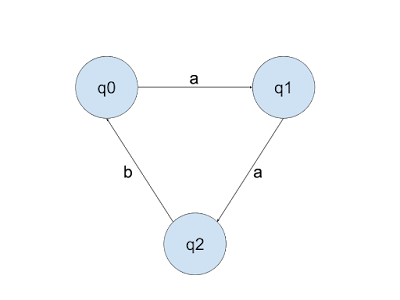
Let Q = {q0, q1, q2} A = {a, b}
Define f: Q x A --> Q as follows:
    (q0, a) --> q1
    (q1, a) --> q2
    (q2, b) --> q0
    (q1, b) --> q1

This is a partial function, not a total function. This is because the function does not include rules for all 6 possible transitions. This may be easier to see if we create a state diagram to illustrate this function.

The state diagram for this function makes it easier to see that there are transition rules missing from the function that we have defined. For example, starting in q0, it is not possible to process the string abaa. We can however process strings like aabab. This function is called non-deterministic. A deterministic function would have rules that describe what to do at each state for each element.

Prove 1 + 2 + 3 + ... + n = n(n+1) / 2 for all n >= 1

Background: This proof is often used for the analysis of various algorithms.

Example: 1 + 2 + ... + 100 = (100 * 101) / 2

If we wanted to write this equality as a part of a program, it could be created as either of the following snippets.

sum = 0
for i = 1 to 100:
    sum += i
print sum

which is the same as

print n * (n + 1) / 2

Both of these code snippets print the same value at the end, and it is possible to mathematically prove which is more efficient.

Now, without further adieu, here is a proof that demonstrates how we can show this.

Prove: 1 + 2 + 3 + ... + n = (n (n + 1)) / 2 for all n ≥ 1.

Base case: Observe 1 = (1 * 2) / 2.
Let k ≥ 1 be some integer.
Assume 1 + 2 + 3 + ... + k = (k (k + 1)) / 2
We want to show that 1 + 2 + 3 + ... + k + (k + 1) = ((k + 1) * (k + 2)) / 2.
Notice that 1 + 2 + ... + k + (k + 1) = (k (k + 1)) / 2 + k + 1 = ((k + 1) * (k + 2)) / 2.

((k + 1) * (k + 2)) / 2 = (k (k + 1)) / 2 + 2 (k + 1) / 2
= (k (k + 1) + 2 (k + 1))
= ((k + 1)(k + 2)) / 2

By the proof of mathematical induction, 1 + 2 + 3 + ... + n = (n (n + 1)) / 2 for all n ≥ 1.

---

From here: Using this same proof technique, it is possible to demonstrate that this is also true for strings. For example, we can prove that (Uⁿ)^R = (U^R)ⁿ.